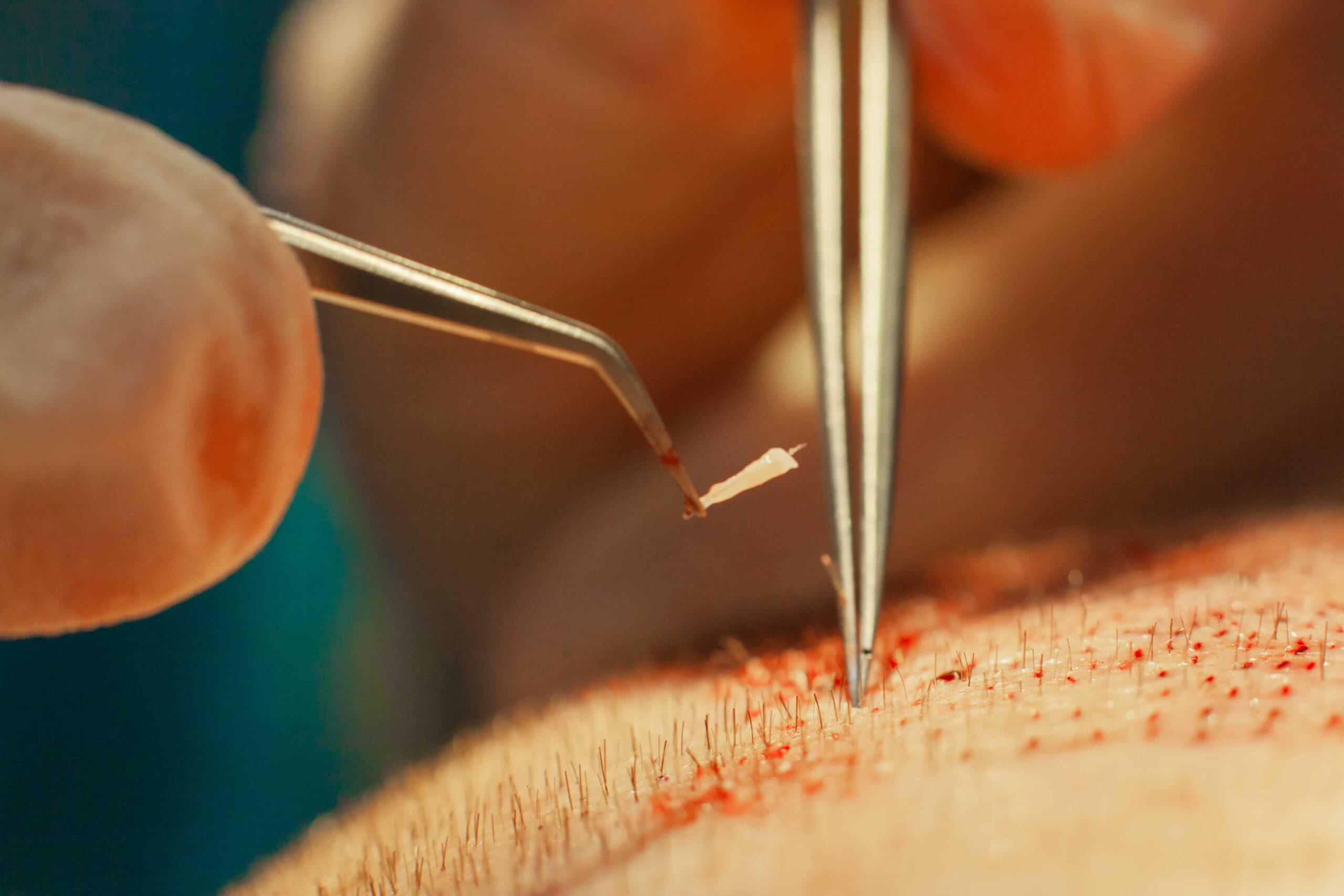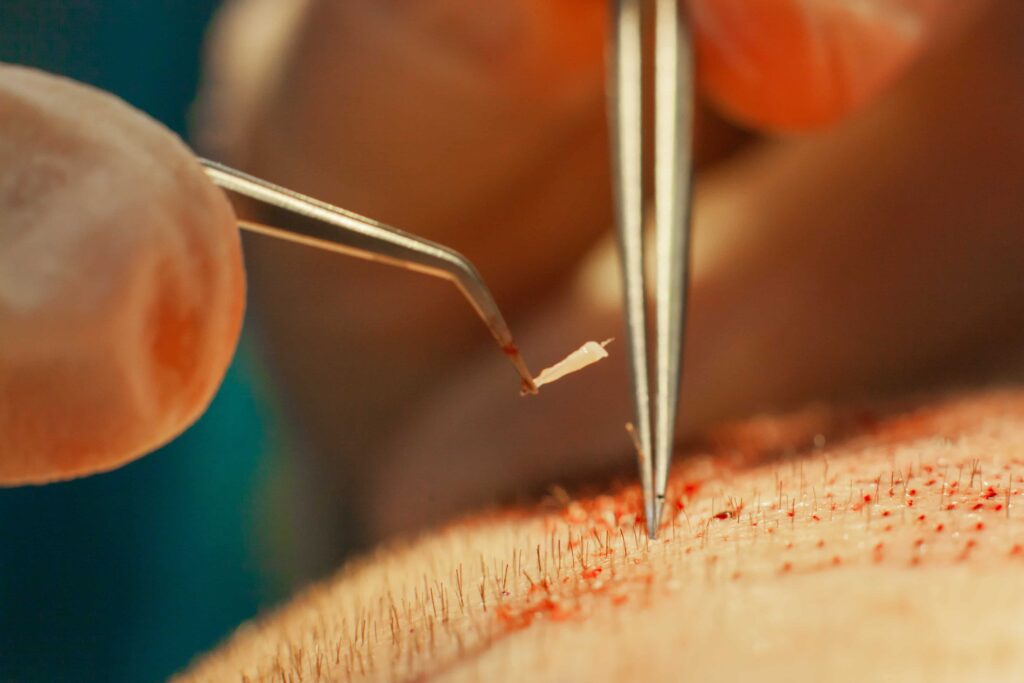
When it comes to hair restoration, transplanting more grafts doesn’t necessarily yield better results. Quite the contrary. Exceeding certain density thresholds can jeopardize graft viability and compromise long-term outcomes.
When we understand the science behind optimal graft density, we can design a treatment plan with the highest potential of success.
In this article, we’ll discuss evidence-backed density thresholds, the risks of overpacking, and modern strategies for maximizing hair count and graft survival.
The Science of Graft Survival
Hair grows in cycles: anagen (growth), catagen (transition), and telogen (resting). Most scalp hair is in anagen. This is the phase we want the transplanted hair to enter after surgery.
It’s normal for transplanted hairs to go into telogen effluvium (shedding) a few weeks post-surgery and then regrow in a new anagen phase around 3–4 months later.
With that at the forefront, we can better manage expectations of our patients. Initial shedding is expected, and true density gains appear gradually as follicles re-enter anagen.

Vascular Limits & Ischemia
The viability of transplanted grafts is fundamentally constrained by the scalp’s vascular capacity.
Each follicular unit functions as a micro-organ implant and must rapidly establish a new capillary network to survive. Under typical conditions, neovascularization begins within 2 to 5 days post-transplantation.
However, when grafts are densely concentrated within a limited surface area, they compete for perfusion. This competition can exceed the available oxygen and nutrient supply, increasing the risk of localized ischemia and subsequent graft failure.
Densities above ~50–60 grafts/cm² risk overwhelming the dermal blood supply. (J Cutan Aesthet Surg)
Exceeding this trauma threshold results in:
- inflammation,
- slows healing,
- and reduces oxygen to grafts.
Grafts are also vulnerable outside the body. They can be damaged by dehydration, rough handling, or high temperatures. These factors increase follicle death.
According to StatPearls (2024), ideal density varies, but survival drops when too many grafts are packed in one area. The authors emphasize that “vascular trauma and oxygen deprivation” are key causes of graft failure.
In clinical practice, transplant density is typically limited to 40–50 grafts per cm² per session to maintain adequate vascular support.
While advanced surgical techniques may allow for higher densities, 60 grafts per cm² is generally regarded as the upper threshold—and only under optimal conditions, such as a well-vascularized scalp and strong donor hair characteristics.
In summary, successful graft survival depends on minimizing mechanical trauma and allowing sufficient time for vascular integration. Meticulous surgical technique is critical to ensure long-term follicular viability and growth.

Measuring Hair Density in 2025
Accurate quantification of hair density—both pre- and post-transplant—is essential for effective surgical planning and outcome assessment.
Advances in diagnostic imaging and analysis have significantly enhanced the precision and objectivity of these measurements compared to earlier methods.
Phototrichograms
Phototrichography remains a gold-standard method for quantifying hair density and growth dynamics. The procedure involves:
- trimming a defined area of the scalp,
- applying a contrast dye to the hair shafts,
- and capturing high-resolution magnified images at baseline and at subsequent time points.
This allows for precise calculation of follicular density (hairs per cm²), hair shaft diameter, and growth rate over the designated interval. (Int J Trichology. )
TrichoScan
TrichoScan is an automated software platform designed for digital phototrichogram analysis. Introduced in the early 2000s, the method involves shaving a standardized scalp area of approximately 1.8 cm², followed by dermoscopic imaging.
The captured images are then processed using AI-assisted algorithms to quantify hair density and differentiate between anagen and telogen phase hairs with high efficiency.(Int J Trichology.)
However, accuracy has been a point of discussion. Some researchers observed that TrichoScan’s automated algorithm tends to slightly under-count density (by ~10%) and over-estimate hair thickness compared to manual evaluation. (Rolf Hoffmann)
Trichoscopy (Dermatoscopy)
Trichoscopy involves examining the scalp and hair under magnification using a digital dermatoscope. It allows clinicians to assess follicle density, identify signs of miniaturization, and evaluate scalp condition in real time.
The technique is widely used to support diagnosis and surgical planning, particularly in cases of patterned hair loss.
While trichoscopy was traditionally used for diagnosing hair and scalp disorders, it is now also applied to quantitatively assess donor area density and the extent of thinning in recipient zones.
Modern Techniques to Maximize Density
Hair restoration techniques have advanced significantly, with a consistent focus on increasing hair density in thinning areas without compromising graft survival.
The following section outlines the primary methods in use today and how each is designed to optimize density while preserving long-term follicular viability.
FUT (Follicular Unit Transplantation)
FUT, often referred to as the “strip method,” involves removing a linear section of scalp from the donor area, which is then microscopically dissected into individual follicular unit grafts for transplantation.
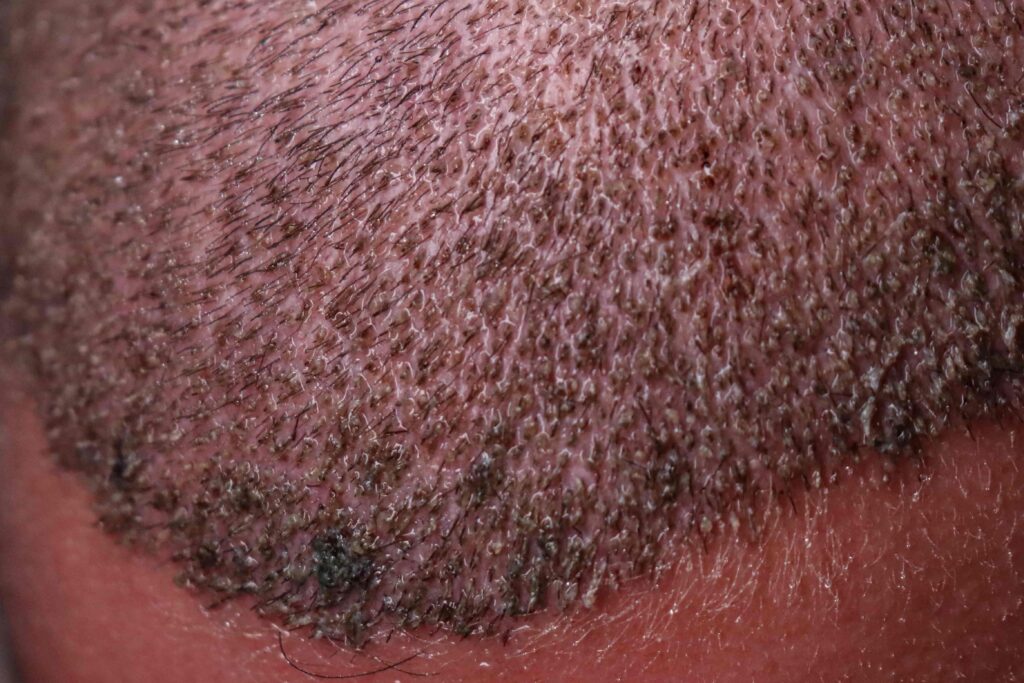
As one of the longest-standing techniques in hair restoration, FUT is valued for its ability to yield a high number of grafts in a single session—typically between 3,000 and 5,000.
This makes it particularly suitable for patients requiring coverage of large balding areas or seeking higher-density outcomes.
The primary limitation of FUT is the linear scar left at the donor site. Although this scar is often narrow and well-concealed—especially when trichophytic closure is used to encourage hair regrowth through the incision—it can restrict the number of FUT procedures that can be performed over time.
FUE (Follicular Unit Extraction)
Follicular Unit Extraction involves the individual harvesting of follicular units using precision punches, typically ranging from 0.8 to 1.0 mm in diameter.
Unlike FUT, FUE does not produce a linear scar; instead, it results in numerous small, dispersed punctate scars across the donor area, which are generally subtle and difficult to detect once healed.
FUE’s rise in popularity is partly due to this minimal scarring, but early FUE had a reputation for slightly lower yield.
Today’s refined FUE techniques (sharper punches, better punch designs, skillful harvesting pattern) have closed that gap – studies show FUE grafts grow as well as FUT grafts when done properly. (David Josephitis)
Sapphire FUE
While not a distinct harvesting technique, this approach represents an advancement in recipient site creation. Rather than using conventional steel blades or needles, surgeons employ sapphire-tipped blades to make precise incisions for graft placement.
Sapphire blades offer superior sharpness and edge retention compared to traditional steel instruments. They produce highly refined, precise incisions, which reduce tissue trauma and allow for closer graft placement.
Long-Hair FUE (U-FUE or No-Shave FUE)
Conventional FUE typically necessitates trimming the donor area to facilitate efficient graft extraction.
In contrast, long-hair FUE is a specialized technique that allows for the removal of follicular units without fully shaving the donor region, thereby preserving the natural length of the hair shafts.
When performed by an experienced surgeon, this method does not compromise graft integrity or survival, as the follicular units remain identical in structure—differing only in the retention of hair length.
Robotic FUE (ARTAS)
The ARTAS system is an advanced robotic platform designed to automate the FUE harvesting process, with newer generations also assisting in recipient site creation.
Its primary contribution to achieving optimal density lies in its ability to deliver consistent, high-precision graft extraction and placement—minimizing variability and potentially reducing the risk of human error during high-volume procedures.
The robot’s optical guidance identifies follicular unit angles and can punch grafts with sub-millimeter accuracy and no fatigue.
A consistent low transection rate (the 2023 study showed ARTAS transected ~13.17% of hairs vs 13.96% by manual FUE, essentially equivalent) (J Cosmet Dermatol) means more viable grafts to implant.
FUT Revisions / Repair Techniques
In the context of optimizing density, it is important to consider how surgeons approach repair cases or patients undergoing multiple transplant sessions.
For individuals with suboptimal outcomes from prior procedures or progressive thinning surrounding a previous transplant, revision surgery can be performed to enhance density.
In cases involving previous FUT, a common strategy involves excising the existing scar to both access additional grafts and improve the aesthetic appearance of the donor site.
Enhancing density in previously transplanted areas is a common component of revision procedures. Once the scalp has adequately healed, additional grafts can be strategically placed between existing ones to improve coverage.
However, overly aggressive density in these regions can compromise surrounding follicles or impair local perfusion.
As such, refinement procedures must be approached with precision and a conservative surgical plan to preserve both existing and newly implanted grafts.
Adjunctive & Non-Surgical Boosters
In addition to surgical technique, a range of adjunctive therapies and supportive strategies can further improve graft survival and enhance the visual outcome of hair restoration.
Platelet-Rich Plasma (PRP)
Platelet-rich plasma (PRP) therapy utilizes autologous blood-derived platelets to support tissue healing and stimulate follicular regeneration. It may be administered preoperatively, intraoperatively, or postoperatively, depending on the clinical protocol.
In a 2015 study involving scarred scalps, PRP-treated areas demonstrated a significant increase in hair density—an average gain of +45.9 hairs/cm²—compared to a reduction of −3.8 hairs/cm² in the placebo group. (Stem Cells Transl Med)
While not every study is universally positive, the consensus is that PRP is a useful adjunct to improve graft survival, especially in challenging cases (e.g. scarring alopecia or low-yield areas).
Exosomes
Exosomes are extracellular vesicles derived from stem cells that play a key role in intercellular signaling and tissue repair.
Although still considered investigational, early clinical studies indicate that exosome-based therapy may enhance hair density and follicular count in both transplanted and native hair by promoting regenerative processes at the cellular level.
A 2023 systematic review noted that in androgenetic alopecia patients, topical or injected exosome treatments significantly increased hair density and thickness without major adverse effects. (J Cosmet Dermatol)
While preliminary results are encouraging—particularly when used in conjunction with platelet-rich plasma—further validation through large-scale, controlled studies is still required before widespread adoption.
Minoxidil & Finasteride
Although these medications do not directly influence graft survival, they play a significant role in optimizing long-term outcomes. Minoxidil may help reduce postoperative shedding and promote faster regrowth by extending the anagen (growth) phase of the hair cycle.
Finasteride, on the other hand, helps preserve native hair by inhibiting dihydrotestosterone (DHT), a key factor in androgenetic hair loss.
Most clinicians recommend initiating finasteride either immediately or shortly after surgery, with minoxidil typically introduced 2 to 3 weeks postoperatively to support overall density maintenance.
Scalp Micropigmentation (SMP)
Scalp micropigmentation (SMP) is a valuable adjunctive option in aesthetic hair restoration. This non-surgical procedure involves depositing pigment into the upper dermis of the scalp to replicate the appearance of natural hair follicles or stubble.
By reducing the contrast between hair and scalp, SMP creates the visual impression of increased density—particularly effective in patients who wear shorter hairstyles.
SMP is commonly used to enhance areas with suboptimal transplant coverage, conceal donor or surgical scars, or provide the appearance of density when additional grafting is not feasible.
Other Boosters
Low-Level Laser Therapy (LLLT) has been proposed to aid in early postoperative healing and improve hair shaft caliber, although clinical evidence remains variable.
Nutritional supplements such as biotin and saw palmetto are often recommended to support overall hair health.
Additionally, modifiable lifestyle factors—including a balanced diet and avoidance of smoking—play an important role in optimizing both surgical outcomes and long-term follicular stability.
FAQs
Can a hair transplant restore my original hair density?
Complete restoration of native density is not typically achievable. Physiological scalp density ranges from approximately 80 to 100 follicular units (FUs) per cm². Transplanted density, by comparison, is generally in the range of 35 to 50 FUs/cm².
However, due to strategic placement and favorable hair characteristics such as shaft diameter and color contrast, this can often produce the visual impression of full coverage.
How many grafts per cm² are typically implanted?
A range of 35 to 40 follicular units per cm² is considered optimal for most cases, balancing aesthetic results with graft survival. Higher densities—up to 50 or even 60 FUs/cm²—may be employed selectively, but only in patients with ideal scalp characteristics.
Will one transplant session be enough for full density?
In many instances, yes. Current techniques allow for the transplantation of 3,000 to 4,000 grafts in a single session, which is sufficient for most patients. According to ISHRS data, approximately 67% of patients report satisfactory outcomes after one procedure.
However, those with extensive balding or a goal of higher density may require a second session to refine results or expand coverage.
Does dense packing of grafts affect survival rates?
It can. Graft survival is directly impacted by vascular supply. Clinical data indicate near-complete survival at densities of 30 grafts/cm², but this rate declines to approximately 84% at 50 grafts/cm².
Dense packing increases the risk of ischemia and delayed healing, particularly when performed in compromised or previously transplanted tissue.
Which method yields the most density: FUT, FUE, or DHI?
All three methods are capable of producing high-density results when executed by an experienced surgeon.
FUT may yield the highest number of grafts in a single session. FUE offers greater flexibility in donor site selection and less visible scarring. DHI allows for precise placement using an implanter pen, but does not inherently increase density.
The choice of technique should be individualized based on donor availability, scalp characteristics, and overall treatment goals.
I’m 6 months post-op, and my density seems low—will it improve?
Not necessarily. Six months represents an early stage in the regrowth timeline. At this point, most patients have achieved approximately 50 to 60 percent of their final result.
Hair growth will continue to evolve over the next 6 to 12 months as follicles mature, shaft diameter increases, and overall density improves.
Book Your Density Analysis – Get Started Today
A comprehensive evaluation is the first step toward achieving optimal hair density. At ForHair, we provide clinically guided assessments using TrichoScan-based analysis—the same objective measurement technology employed in clinical research to evaluate hair density, follicular units, and growth dynamics.
Remote consultations are available, offering convenient access to medically informed planning tailored to individual patient profiles.
| Precision planning. Evidence-based care. Personalized to you. BOOK YOUR FREE CONSULTATION |
Sources:
- Marwah MK, Mysore V. Recipient Area. J Cutan Aesthet Surg. 2018 Oct-Dec;11(4):202-210. doi: 10.4103/JCAS.JCAS_124_18. PMID: 30886474; PMCID: PMC6371721.
- Zito PM, Raggio BS. Hair Transplantation. [Updated 2024 Feb 12]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan-. Available from: https://www.ncbi.nlm.nih.gov/books/NBK547740/
- Dhurat R, Saraogi P. Hair evaluation methods: merits and demerits. Int J Trichology. 2009 Jul;1(2):108-19. doi: 10.4103/0974-7753.58553. PMID: 20927232; PMCID: PMC2938572.
- Rolf Hoffmann and Holger Lüdtke TrichoScan®, Vol 1 https://trichoscan.com/media/files/TrichoScan_Montagnas_trichology_vol_I.pdf
- Josephitis, David, and Ron Shapiro. “FUT vs. FUE Graft Survival: A Side-By-Side Study of 3 Patients Undergoing a Routine 2,000+ Graft Hair Transplantation.” International Society of Hair Restoration Surgery, vol. 28, no. 5, Sept. 2018, pp. 179–182, https://doi.org/10.33589/28.5.0179.
- Zhu Y, Yang K, Lin JM, Ni C, Zhang Y, Li Z, Liu Q, Zhou Y, Lin J, Wu W. A Comparative Study on the Application of Robotic Hair Restoration Technology Versus Traditional Follicular Unit Excision in Male Androgenetic Alopecia. J Cosmet Dermatol. 2024 Dec;23(12):4213-4222. doi: 10.1111/jocd.16554. Epub 2024 Sep 19. PMID: 39297414; PMCID: PMC11626372.
- Gentile P, Garcovich S, Bielli A, Scioli MG, Orlandi A, Cervelli V. The Effect of Platelet-Rich Plasma in Hair Regrowth: A Randomized Placebo-Controlled Trial. Stem Cells Transl Med. 2015 Nov;4(11):1317-23. doi: 10.5966/sctm.2015-0107. Epub 2015 Sep 23. PMID: 26400925; PMCID: PMC4622412.
- Gupta AK, Wang T, Rapaport JA. Systematic review of exosome treatment in hair restoration: Preliminary evidence, safety, and future directions. J Cosmet Dermatol. 2023 Sep;22(9):2424-2433. doi: 10.1111/jocd.15869. Epub 2023 Jun 28. PMID: 37381168.
- International Society of Hair Restoration Surgery: 2025 Practice Census Results. 2025. https://ishrs.org/wp-content/uploads/2025/05/report-2025-ishrs-practice-census_05-12-25-final.pdf